How to find holes in the universe

How do you know the room you are reading this article in does not have a hole? Not its walls, floor, or ceiling, but the room itself. What if somebody removed a small portion of the universe from inside this room? There is no way you can see or access the missing bit of space; after all, we live inside the universe, and we have no concept of what lies outside it (and it turns out we don’t need it!). The mathematical question behind this is ‘how can we analyse the shape of a space without looking at it from the outside?’ Such a space could be a physical region in which particles move and interact, all possible configurations of a mechanical system (e.g. a robot arm) or a molecule (e.g. some complicated protein or knotted DNA), or indeed our universe.

A good approach to detect a hole in your room is to try and wrap something around it. In fact, this simple idea is so powerful that it lies at the foundations of the area of Algebraic Topology. To illustrate this, let’s think about how can we find a hole in a sheet of paper, pretending that we only have access to the two-dimensional plane of the paper itself. In that world we can place a piece of string in the shape of a loop and then make this loop smaller and smaller by pulling the string. We will be able to perfectly shrink our loop until it becomes a single point in the plane if, and only if, there is no hole in the paper which is enclosed by our loop!

To wrap and detect holes in higher dimensions, we ask not only whether we can shrink one-dimensional loops to a single point, but also two-dimensional spheres (think a balloon losing air) and spheres of any higher dimension. This turns out to give us an extremely rich set of information about the shape—or topology—of our space (namely its so-called homotopy groups).

Part of the motivation for my research stems from a beautiful, geometric way of studying those features of spaces which are detectable using one-dimensional loops. The key concept is called parallel transport; it plays an important role in Differential Geometry, Einstein’s General Relativity and particle physics.

Here is a one-paragraph crash course on parallel transport: a parallel transport is a rule for how we transport and compare data along any path in our space (by solving a particular differential equation). It needs to be such that if we cut a path into two smaller pieces, transporting data along the first piece and then along the second is the same as transporting along the entire path. Given any two points x and y in our space, the parallel transport along two different paths from x to y will, in general, be different. Some parallel transports, however, have the property that they give the same result whenever the two paths can be deformed into each other without breaking or cutting them. These parallel transports are called flat. (In General Relativity the failure of a certain parallel transport to be flat provides a measure for the mysterious curvature of space-time.)

Now suppose we have some type of data attached to each point in our space, together with a given parallel transport for this type of data. Pick any point x in our space. If we have a path that starts and ends at x (i.e. a loop), parallel transport around it will translate data at x into data at x, but this process might properly change the data! For instance, it might rotate the entire data set. However, if our parallel transport is flat and if we can shrink the loop to a point, then the transport around this loop does nothing to the data. If we cannot shrink the loop to a point—i.e. if there is a hole inside it—transporting around the loop might still produce a non-trivial transformation of our data. The crucial insight is that going around a loop using a flat parallel transport can result in a non-trivial transformation only if there is a hole somewhere inside our loop! In that way, flat parallel transports allow us to test whether a given loop contains a hole.

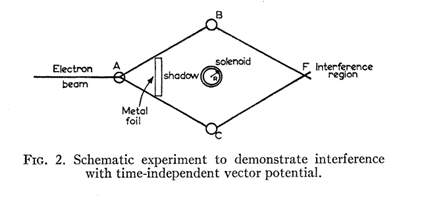
A great example of this concept, which revolutionised the world of physics in 1959, is the Aharonov-Bohm effect: here, very roughly speaking, we take the two-dimensional plane with a hole somewhere. Inside the hole, and only there, we generate a magnetic field perpendicular to the plane. An electron passing along any loop which encloses the hole feels a measurable effect by the magnetic field, even though it never passes through a region where the magnetic field itself is actually non-zero!

An important question I address in my research is how to extend the idea of parallel transport to higher-dimensional objects so that we can use tools from Geometry to study higher-dimensional phenomena in Topology. Parallel transport around loops as above has only limited power: for instance, each loop on the two-dimensional sphere can be shrunk to a point, even though the sphere has a hole (it is hollow!). So one-dimensional loops are unable to detect this hole. Rather, we would need to be able to also transport data along two-dimensional surfaces to detect the hole inside the sphere. Conceptually, this has striking resemblance with certain aspects of string theory, and this has been helpful in the development of two-dimensional parallel transport in the past.

Developing even higher-dimensional cases requires bringing together recent technology from several branches of mathematics such as homotopy and higher category theory, field theory and deformation theory. Fully understood, higher-dimensional parallel transport will not only help us study the topology of spaces at a conceptual level. It also has direct applications in physics, such as to topological phases of matter, and I have recently met colleagues here in Oxford who already apply two-dimensional parallel transport to improve machine learning. In short, developing higher-dimensional parallel transport requires linking several branches of mathematics, but will help advance several branches of science. That, to me, is one of the main fascinations of this topic.