Make Your Own Pi
14 Mar 2020|Tom Crawford
- Research
March 14th is Pi Day, and as of 2020 is also the official UNESCO International Day of Mathematics. You may be wondering what’s so special about a seemingly random day in the middle of March, and if you’re not from the US then you’re completely right to do so. The key is in the date. March 14th is written as 3-14 using the US system, which just so happens to be the first three digits of the number Pi which is 3.14 to two decimal places. If we use the UK system, then we’d need 31-4, or the 31st April, which unfortunately isn’t a real date in the Gregorian calendar. So, March 14th it is.
But why Pi? Even as a mathematician this might seem a random choice of number to represent the International Day of Mathematics, at least until you ask yourself the following question: which single well-known number best represents the field of mathematics? As an applied mathematician (not too dissimilar to a physicist or engineer) my choice would be the number e – Euler’s number. It’s certainly a great representation of all-things calculus (and therefore pretty much any equation in physics), but well-known outside of the mathematical community? I’m not so sure. And herein lies the reasoning behind the choice of Pi. There may be more important numbers (and please do let me know which one you’d pick if in charge), but better-known I highly doubt it. So, Pi it is.
Now we’ve got a better feel for the day named after the number, let’s talk about Pi itself. You may know it in terms of circles, but it has the rather fantastic knack of cropping up in the most unexpected places… Quantum Theory? Check. Einstein’s Theory of Relativity? Check. Newton’s Law of Gravity? Check. Three of the most important theories we use to explain the universe, and each of them has a formula containing the number Pi.
Quantum: Heisenberg’s Uncertainty Principle
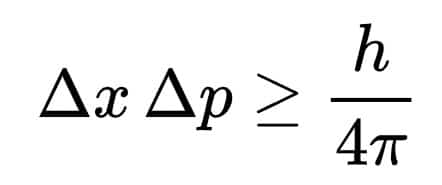
Relativity: Einstein Field Equations
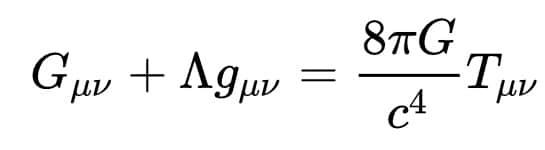
Gravity: Newton’s Gravitational Constant
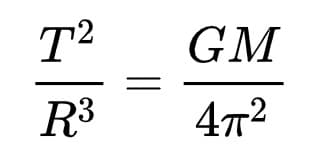
This ‘superhero-like’ ability to appear everywhere means that we can have a lot of fun with how we define the number Pi. The standard definition is to use circles: the perimeter of the circle or circumference, c, is equal to Pi multiplied by the distance across the circle passing through the centre or the diameter, d.
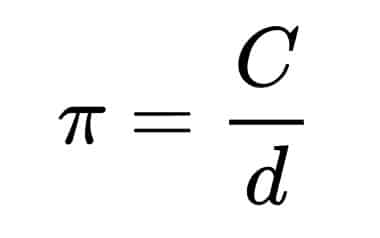
We can make things a little more complicated by thinking about the other circle-based formulas that contain Pi and using them to define its value instead. For example, the volume of a sphere, V, is equal to 4/3 times Pi times the radius, r, cubed. Rearranging, we define Pi as follows:
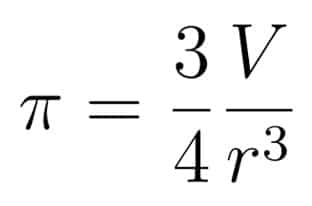
Now, here’s the best bit. Since Pi appears in the formula for the volume of a sphere, it means that any calculation involving the need to work out the volume of a spherical object will include the number Pi, and that means we can rearrange any such formula to get a new definition. Here’s one for you:
π = (3 x weight of Titanic)
—————————————-
(4 x number of ping-pong balls required to lift the Titanic x density of the Atlantic Ocean
x weight of a ping-pong ball x (radius of ping-pong ball)3)
Don’t believe me? Here’s how it works…
We want to know the answer to the question: how many ping-pong balls will it take to lift the Titanic from the ocean floor? The idea being that each ping-pong ball floats, and therefore has a positive buoyancy force (don’t worry too much about exactly what that means other than the fact that objects which float have a positive buoyancy force and those which sink have a negative buoyancy force). If we calculate the buoyancy force on a single ping-pong ball, then that will in fact tell us the amount of weight that each individual ball is able to support before it sinks. Think of doing the following experiment with a boat. If the boat is empty, then it will float. As you start to add weight, it moves down lower and lower into the water until eventually you’ve added so much weight that it is completely submerged and sinks down to the bottom of the lake. The total amount of weight that you added up until the moment before it’s submerged is equal to the maximum amount of weight that the boat is able to support. That weight is the positive buoyancy force of the empty boat.
In our boat experiment we can keep track of the weight we are adding to the boat, but with a ping-pong ball it isn’t quite so simple. Instead, we have to calculate the buoyancy force using a neat idea called ‘Archimedes Principle’. We don’t need to worry about the exact details, just that we have a formula for the buoyancy force courtesy of Archimedes (yes, the guy that ran naked through the streets of Ancient Greece). Archimedes Principle tells us that the buoyancy force of an object is equal to the weight of water displaced by the same object. And what this means in practice, is we just need to multiply the volume of a ping-pong ball by the density of the Atlantic Ocean to get the weight that a single ping-pong ball can support:
Volume = 4/3 x Pi x radius3 = 4/3 x 3.14 x 23 = 33.5 cm3
Density of Atlantic Ocean = 1.027 g/cm3
Weight supported by 1 ping-pong ball = 33.5 x 1.027 = 34.4 g
At this point we must remember to subtract the weight of the ping-pong ball itself, to give the amount that we can ‘add’ before it starts to sink:
Total weight that can be lifted by 1 ping-pong ball = 34.4 – 2.7 = 31.7 g
Finally, the weight of the Titanic is 47,500,000,000 g and so the total number of ping-pong balls required to lift it is given by:
47,500,000,000 / 31.7 = 1.498 billion
(I’m aware I’ve taken you on a slight detour from our original topic of Pi, but I hope you’ve at least been able to follow the main ideas of the calculation. If you would like to see more details of how it all works, then you can watch me run through the solution in full in this video.)
So, with only 1.498 billion ping-pong balls we can lift the Titanic from the depths of the Atlantic Ocean and display it for all to see in a museum. If only it were so simple… Whilst the calculation is itself entirely correct, there’s something we’ve missed. The idea of using ping-pong balls was a real suggestion put forward by a group of scientists in the 1970’s, which needless to say did not happen. If you think you have an idea why get in touch via the contact form on my website.
This is no doubt a rather surprising and hopefully interesting result, but remember we only got to ping-pong balls and the Titanic because we were thinking about fun ways to define the number Pi. Looking back through our calculations, you’ll see that Pi appeared when working out the volume of a ping-pong ball, and so by putting all of our calculations together and rearranging the equation (like we did for the volume of a sphere) we end up with the brilliant (and my all-time favourite) definition:
π = (3 x weight of Titanic)
—————————————–
(4 x number of ping-pong balls required to lift the Titanic x density of the Atlantic Ocean
x weight of a ping-pong ball x (radius of ping-pong ball)3)
With Pi Day and the first ever International Day of Mathematics fast approaching, why not celebrate the wonderful world of numbers by creating your very own definition of Pi. As you’ve seen with the example above, all you need is a calculation involving circles or spheres and some rearranging to get the tastiest number all by itself. Give it a go and let me know how you get on! @tomrocksmaths
Category: Research
Author

Tom
Crawford
Dr Tom Crawford is a Fellow by Special Election in Mathematics at St Edmund Hall with a mission to share his love of maths with the world. His award-winning website features videos, podcasts, articles and puzzles designed to make maths more entertaining, exciting and enthralling for all. Whether he’s performing live as the Naked Mathematician with Equations Stripped, telling you the fun facts about numbers that you didn’t realise you’ve secretly always wanted to know with his Funbers series on the BBC, or getting another maths tattoo (6 and counting), it’s safe to say Tom is always finding new ways to misbehave with numbers!
You can find more maths-based fun on Tom’s award-winning website and follow him on Facebook, Twitter, YouTube and Instagram @tomrocksmaths for the latest updates.