An introduction to research in Computational Complexity Theory
26 Jun 2019|Leslie Ann Goldberg
- Research
Computational complexity theory is a mathematical research area in which the goal is to quantify the resources required to solve computational problems. It is concerned with algorithms, which are computational methods for solving problems.
- Some computational problems are so difficult that we can prove that no fast algorithm exists for solving them. This means that, no matter how clever people are in the future, we will never think of a fast algorithm for solving any of these problems – such algorithms do not exist. An example of such a hard problem is determining whether one of the players has a winning strategy from a given position in a version of the game of draughts.
- Many other computational problems do have fast algorithms, even if the obvious algorithms are slow. For example, nobody knew a fast algorithm for testing whether a number is prime until 2002, though a fast algorithm does exist.
- Often, we study computational problems that we can’t place into either of these two categories, and we study such problems by comparing their difficulties, relative to each other. The most well-known way to do this involves the theory of “NP-completeness”. There are thousands of computational problems that have been proved to be “NP-complete”. Although we don’t know whether these problems have fast algorithms, we do know that all of them are equivalently difficult, so either all of them have fast algorithms, or none of them do. Proving that a problem is “NP-hard” establishes that this problem is so difficult that the existence of a fast algorithm for solving this problem would also imply the existence of a fast algorithm for solving every single problem in NP. Thus, NP-hardness is viewed as strong evidence that the problem has no fast algorithm.
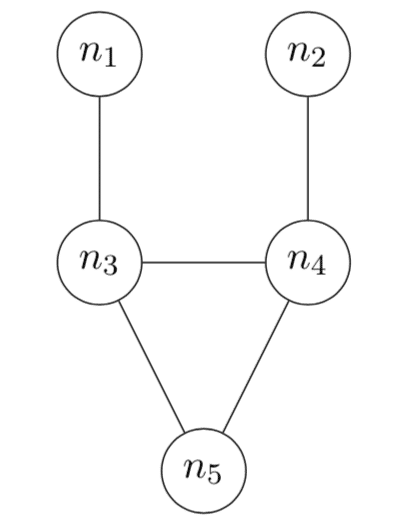
In this blog entry, I have been asked to tell you about one recent research result. The goal is to give you an idea about the type of research that mathematical computer scientists do. The blog entry won’t require any special background, but I do need to explain the concept of a graph. This is just a collection of nodes in which some pairs of nodes are connected by edges. You can get the idea from the example in the following picture, where the nodes are $n_1$, $n_2$, $n_3$, $n_4$ and $n_5$. There are 5 edges, for example, one from node $n_1$ to node $n_3$.
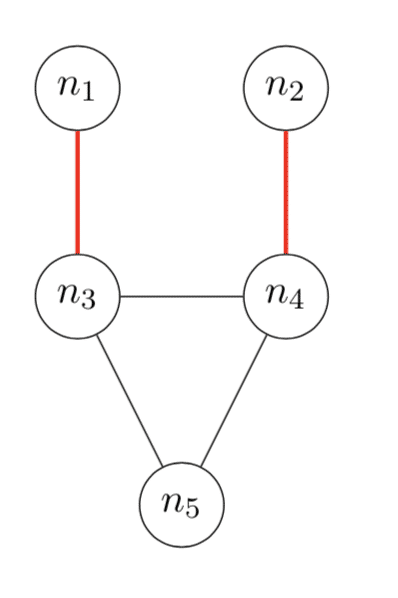
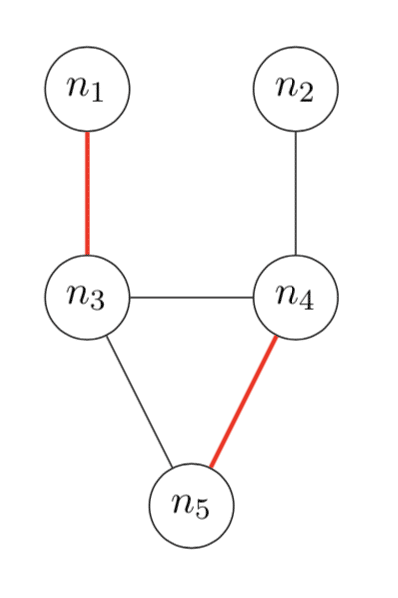
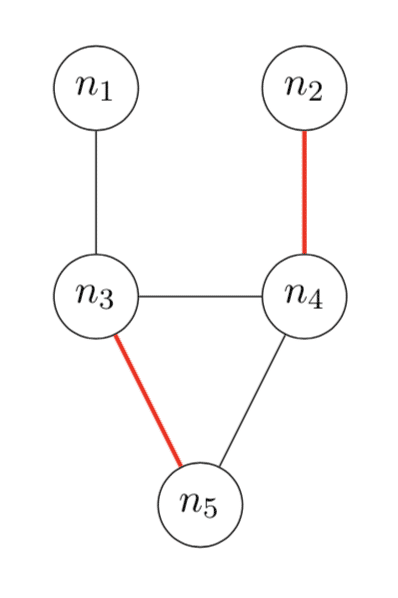
Now I want to tell you about dimers. These were apparently first studied in chemistry in the 1930s (see the discussion in Heilmann and Lieb’s paper) but I will just define them from a mathematical point of view. A dimer is something that covers an edge of a graph. A dimer arrangement is a collection of dimers such that no node touches more than one dimer. The next picture shows three dimer arrangements of the graph that we saw before. Each of these dimer arrangements has two dimers. (For example, in the first picture there is one dimer covering the edge from node $n_1$ to node $n_3$ and another covering the edge from $n_2$ to $n_4$.) Since this graph has five edges, there are also five dimer arrangements with exactly one dimer. There is also a dimer arrangement with no dimers. We have now accounted for all of the dimer arrangements of this graph – there is no way to put more than two dimers on the graph without overlap.
Now to get to the point. A dimer arrangement with $k$ dimers has a weight which we write as $x^k$, where $x$ is a variable representing the contribution of an individual dimer. The dimer partition function is the sum of the weights of all dimer arrangements. So for this graph, the dimer partition function is $f(x) = 1 + 5x + 3x^2$. That is because there is $1$ dimer arrangement with no dimers and this arrangement has weight $x^0=1$. There are $5$ dimer arrangements with a single dimer, and these each have weight $x^1 =x$. Finally, there are $3$ dimer arrangements with $2$ dimers, and these each have weight $x^2$.
Now let’s go back to computational problems. The computational problem that I have in mind is that of computing the dimer partition function. Given some fixed value of $x$, the input to the problem is a graph, and the output is the value $f(x)$ of its dimer partition function. Obviously, for any $x$, it is easy to compute the partition function of the graph in the picture above, because we can compute $1 + 5x + 3x^2$. We don’t even need a computer for that. We just consider each dimer arrangement, and add up the weights. The problem with this approach is that, if the graph has many nodes, then the number of dimer arrangements is too large to allow considering them one-by-one. For example, there are graphs with just over 100 nodes for which the number of dimer arrangements is more than the number of atoms in the known universe! Restricting the class of graphs doesn’t help much. A graph is said to be “$d$-bounded” if every node touches at most $d$ edges. The graph in our pictures above is $3$-bounded. Anyway, there are $2$-bounded graphs with only 400 nodes that still have more dimer arrangements than the number of atoms in the known universe.
What I actually want to discuss in this blog entry is whether there is a fast algorithm for approximately computing the dimer partition function. I’m not going to say precisely what I mean by “approximate”. Let’s just say, for the purpose of this blog, that “to approximate” means “to get within 99.99% of the right answer”. Note that this is still a really daunting task. If the number of dimer arrangements is more than the number of atoms in the universe, then a computer certainly doesn’t have time to examine 99.99% of them (or even 0.01% of them).
OK – so does this computational problem have a fast algorithm? It turns out that the answer depends on $x$, and on the kind of graphs that we consider. Consider $3$-bounded graphs. Combining our new result with results in the literature (such as this, this, and this) it turns out that, for any $x> -1/8$ there is a fast algorithm for approximating the dimer partition function, but for any $x< -1/8$ the approximation problem is NP-hard. Actually, it is “#P-hard”, which is an even stronger form of computational hardness which implies NP-hardness.
It seems strange that the difficulty of the approximation problem changes so radically at $x=-1/8$ but the reason for this relates to the fact that the dimer partition function can only be $0$ if $x< -1/8$. The result extends to the case where $x$ is a complex number such as $3 + 4i$. It turns out that for every complex $x$ (except when $x$ is a a real number less than $-1/8$) there is a fast approximation algorithm. The result also extends to $d$-bounded graphs. The approximation is easy unless $x$ is a real number less than $-1/(4(d-1))$.
In addition to considering the $d$-bounded case, Bezáková, Galanis, Štefankovič and I studied the approximation problem on a wider class of graphs, by not restricting the number of edges that a node can touch. We studied the class of graphs with connective constant at most $d$ which, very informally, means that “on average” a node touches at most $d$ edges, though some nodes can touch more. This had been studied previously when $x$ is positive and real. We discovered good approximation algorithms for all $x$ except negative reals and proved that, for any negative real number, there is a negative real number $x$ arbitrarily close to this one, at which the approximation problem is #P-hard.
Approximating the dimer partition function is just one example of the sort of computational problem that we study. By studying these, our real objective is to understand computation, and in particular to understand how varying parameters ultimately determines which computational problems are feasibly solvable, and which, provably, are not.
Read more on our blog
Category: Research
Author

Leslie Ann
Goldberg
Leslie Ann Goldberg is a Senior Research Fellow at St Edmund Hall and is the Head of the Department of Computer Science at Oxford.

